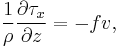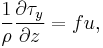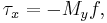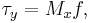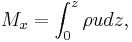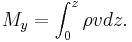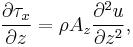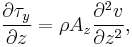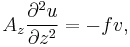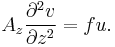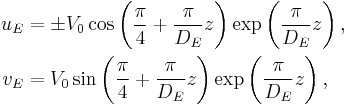Ekman transport
Ekman transport, part of Ekman motion theory first investigated in 1902 by Vagn Walfrid Ekman (for whom it is named), is the term given for the 90 degree net transport of the surface layer (depth to which wind penetrates) due to wind forcings. This phenomenon was first noted by Fridtjof Nansen, who recorded that ice transport appeared to occur at an angle to the wind direction during his arctic expedition during the 1890s.[1] The direction of transport is dependent on the hemisphere. In the northern hemisphere this transport is at a 90 degree angle to the right of the direction of the wind, and in the southern hemisphere it occurs at a 90 degree angle to the left of the direction of the wind.[2]
Contents |
Theory
Ekman theory explains the theoretical state of circulation if water currents were driven only by the transfer of momentum from the wind. In the physical world this is difficult to observe due to the presence of many other current driving forces (i.e. pressure and density gradients). Though the following theory technically applies to this ideal situation in which only wind drives circulation, Ekman motion describes the wind driven portion of surface circulation seen in the surface layer.[3][4]
Surface currents flow at a 45 degree angle to the wind due to a balance between the Coriolis force and the drags generated by the wind and the water.[5] If the ocean is divided vertically into thin layers, the magnitude of the velocity (the speed) decreases from a maximum at the surface until it dissipates. The direction also shifts slightly across each subsequent layer (right in the northern hemisphere and left in the southern hemisphere). This is called the Ekman spiral.[6] The layer of water from the surface to the point of dissipation of this spiral is known as the Ekman layer. If all flow over the Ekman layer is integrated, the net transportation is at an angle of 90 degrees to the right (left) of the surface wind in the northern (southern) hemisphere.[2]
Mathematical derivation
Some assumptions of the fluid dynamics involved in the process must be made in order to simplify the process to a point where it is solvable. The assumptions made by Ekman were:[7]
- no boundaries;
- infinitely deep water;
- eddy viscosity,
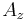 , is constant (this is now known not to be totally true);
, is constant (this is now known not to be totally true); - the wind forcing is steady and has been blowing for a long time;
- barotropic conditions with no geostrophic flow;
- the Coriolis parameter,
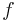 is kept constant.
is kept constant.
The simplified equations for the Coriolis force in the x and y directions follow from these assumptions:
where 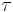 is the wind stress,
is the wind stress, 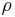 is the density,
is the density, 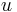 is the East-West velocity, and
is the East-West velocity, and 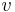 is the north-south velocity.
is the north-south velocity.
Integrating each equation over the entire Ekman layer:
where
Here 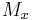 and
and 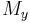 represent the zonal and meridional mass transport terms with units of mass per unit time per unit length. Contrarily to common logic, north-south winds cause mass transport in the East-West direction.[8]
represent the zonal and meridional mass transport terms with units of mass per unit time per unit length. Contrarily to common logic, north-south winds cause mass transport in the East-West direction.[8]
In order to understand the vertical velocity structure of the water column, equations 1 and 2 can be rewritten in terms of the vertical eddy viscosity term.
where 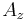 is the vertical eddy viscosity coefficient.
is the vertical eddy viscosity coefficient.
This gives a set of differential equations of the form
In order to solve this system of two differential equations, two boundary conditions can be applied:
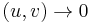 as
as 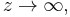
- friction is equal to wind stress at the free surface (
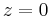 ).
).
Things can be further simplified by considering wind blowing in the y-direction only. This means is the results will be relative to a north-south wind (although these solutions could be produced relative to wind in any other direction):[9]
where
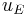 and
and 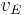 represent Ekman transport in the u and v direction;
represent Ekman transport in the u and v direction;- in equation 3 the plus sign applies to the northern hemisphere and the minus sign to the southern hemisphere;
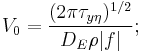
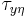 is the wind stress on the sea surface;
is the wind stress on the sea surface;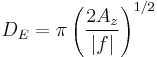 is the Ekman depth (depth of Ekman layer).
is the Ekman depth (depth of Ekman layer).
By solving this at z=0, the surface current is found to be (as expected) 45 degrees to the right (left) of the wind in the Northern (Southern) Hemisphere. This also gives the expected shape of the Ekman spiral, both in magnitude and direction.[9] Integrating these equations over the Ekman layer shows that the net Ekman transport term is 90 degrees to the right (left) of the wind in the Northern (Southern) Hemisphere.
Applications
- Ekman transport is a factor in coastal upwelling regimes which provide the nutrient supply for some of the largest fishing markets on the planet.[10] Wind in these regimes blows parallel to the coast (such as along the coast of Peru, where the wind blows North). From Ekman transport, surface water has a net movement of 90 degrees to the left in such a location. Because the surface water flows away from the coast, the water must be replaced with water from below.[11] It is important to remember that in shallow coastal waters, the Ekman spiral is normally not fully formed and the wind events that cause upwelling episodes are typically rather short. This leads to many variations in the extent of upwelling, but the ideas are still generally applicable.[12]
- Ekman transport is similarly at work in equatorial upwelling, where, in both hemispheres, a trade wind component towards the west causes a net transport of water towards the pole, and a trade wind component towards the east causes a net transport of water away from the pole.[10]
- On smaller scales, cyclonic winds induce Ekman transport which causes net divergence and upwelling, or Ekman pumping,[10] while anti-cyclonic winds cause net convergence and downwelling, or Ekman suction[13]
- Ekman transport is also a factor in the circulation of the ocean gyres. Ekman transport causes water to flow toward the center of the gyre in all locations, creating a sloped sea-surface, and initiating geostrophic flow (Colling p 65). Harald Sverdrup applied Ekman transport while including pressure gradient forces to develop a theory for this (see Sverdrup balance).[13]
See also
Notes
References
- Colling, A., Ocean Circulation, Open University Course Team. Second Edition. 2001. ISBN 978-0-7506-5278-0
- Knauss, J.A., Introduction to Physical Oceanography, Waveland Press. Second Edition. 2005. ISBN 978-1-57766-429-1
- Mann, K.H. and Lazier J.R., Dynamics of Marine Ecosystems, Blackwell Publishing. Third Edition. 2006. ISBN 978-1-4051-1118-8
- Pond, S. and Pickard, G. L., Introductory Dynamical Oceanography, Pergamon Press. Second edition. 1983. ISBN 978-0-08-028728-7
- Sverdrup, K.A., Duxbury, A.C., Duxbury, A.B., An Introduction to The World's Oceans, McGraw-Hill. Eighth Edition. 2005. ISBN 978-0-07-294555-9
External links
|
||||||||||||||||